Summer of Math Exposition

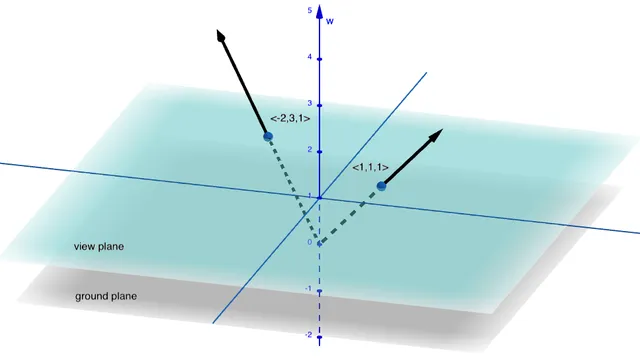
This idea that vectors can represent two different things is called a dual representation or just duality.

This is the first time I felt I understood this “duality” thing, valuable lesson there, maybe could be interesting to link it to other occurrences of duality in math

Beside this, i got a bit lost between the notations but that’s a problem due to lack of attention on my side.

This blog post has an immense potential to get translated into a similar narrative video, because the illustrations are not always crystal clear and some more interactive animations could help a lot with this

Main piece of feedback here is to supplant your assertion that 3D projective space is easy to understand given understanding of 2D projective space with examples. The essay was a good intro into projective space for 1D/2D but your claim at the beginning — that understanding projective geometry in 1D/2D helps with 3D didn’t really have any examples supporting it.

Great explainer! This is obviously a subject which has seen a lot of explanations already, but you do take a slightliy different approach here. I like the new terms you define (like equation vector), they’re completely motivated and you are clear that they’re idiosyncratic. The examples are good to have to, however I personally feel like the examples are too many.. Maybe if the calculations had been an explicit focus of the article then the intersection of a ray and a line segment would be more deserving of its place.

“and why they’re called homogeneous coordinates” -> “and that’s why they’re called homogeneous coordinates”

There are a lot of cases and equations to look through, so it’s useful as an intro to view a broad scope. It will definitely take time to go through (too many all at once)

Not one thing, but the combination of clear visualization with comprehensive coverage is impressive.

Interesting topic. the layout can be improved

I enjoyed this explanation and thought that the diagrams were especially useful. 3D is notoriously difficult to show but you picked good angles to show the intersecting planes. The animated diagrams were great too.

However I did struggle to follow the algebra at times, especially when you introduced the alternative notation with tildes and angle brackets. I was still able to understand but I don’t think I fully grasped the underlying maths with a deep understanding.

I liked the presentation of moving from 1 to 2 to 3 dimensions gradually, and it was a nice narrative arc. I don’t think it was entirely novel because it reminded me of the 3b1b video on quaternions. I think adding interactivity and more videos (like in the quaternion explainer) would have helped a lot here too because it is a similar topic and both are useful in games programming. Overall I enjoyed the entry though!

Amazing content! The aesthetics of the page feel somewhat dated.

This article makes for some of the best reference material I have seen in a while, Breaking down the Basic Maths involved in 3D graphics.

Ultimately, the article felt rather text-booky. With Maths communication being the Goal, I don’t think this article implemented tried to step outside the comfort Zone of a Standard blog article.

Article started with “Most introductions to the math of 3D graphics I’ve come across immediately get caught up in the details of why we use vectors with four ” Article ended with: “For an essay claiming to explain the math of 3D graphics, I’m going to spend very little time actually talking about 3D projective space.”

I understand the article’s approach with “But I think there’s also value in slowing down a bit.” but I really would have liked the mapping of what we learned here applied to examples used in 3D graphics, as that is the premise of our journey here.

I really enjoyed how the personal Story of the Reader was invovled and their journey in understanding some Points with passages like “This confused me for ages. I knew that it was a problem and I knew mechanically how to correct the problem. But the reason why it was a problem bugged me.”.