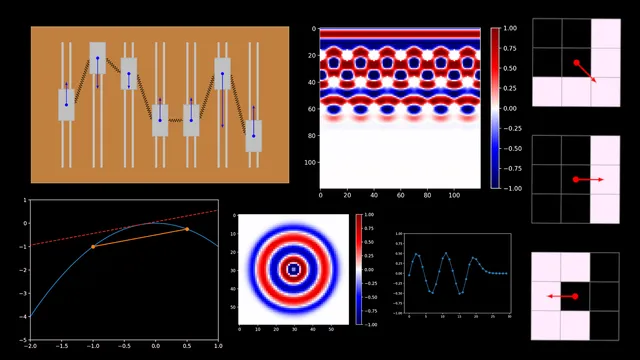
Exploring the wave equation
In this article, we derive and examine the wave equation in both its pure and discretized form. Finally, we build a functioning wave simulation, which allows more complex behaviour such as interaction with objects.
Analytics
Comments
4.3
You get pretty deep into the formulas with not a ton of clear payoff. A less numerate audience might have a hard time pushing through. Great visuals (maybe add a visual indication of where the bollards are), might benefit from some more user control on playback.
8.6
One of the best entries I've seen so far! Very impressive animation and coding work, especially with you actually putting the code in the article itself! And I loved the story with Bob too, the asides about partial derivatives etc, very easy to follow. Truly marvellous, you should really be proud :)
5.4
I feel like there’s an opportunity here to really dive into Bob’s problem. The math is a bit dry - I understand that’s the main purpose of the presentation. But opening with the problem, and ending with “Bob plays around with the software and finds something he’s happy with” left me wanting more.
6.5
Very nice article. The only problem is reader should better have a good calculus knowledge to understand the notation and the logic.
8.2
The author had a clear and interesting motivation for the problem/theme.
They also used many visualizations with their code, which made it easy to follow along.
The article is also well structured in that the previous motivate the next sections.
Additionally the use of external sources/videos was a clever way to complement and to elevate the blog.
The use of formal math was imo the right amount as it allows interested viewers to dive deeper, but the main goal/content of the article can still be enjoyed.
Another plus point were Bob's mathematical fun facts since they further explained the mathematical concepts used while still staying in the narrative
As for possible improvements:
It seems that the code displayed is cut off at some points (may be device problem);
It would be a nice (possibly very time intesive to set up) to run and adjust the code on the website (it is also mentioned on the 'interactive software' checkpoint);
Overall I thoroughly enjoyed the article, and a lot of effort must've went into it and it shows
7.2
Oh poor Bob...
Minor thing I was confused about is why you had to use d<3 condition for the two-dimensional case, while for 1D you just varied the pos[0]. wouldn't just d<1 make the same sort of wave.
Other than that, great entry.
9
This is an excellent exposition. Truly enjoyable.
5.7
Loved it! I’m not quite sure why we needed to switch to the midpoint definition for the difference quotient though… Figure 5 doesn’t prove anything, because as you shrink delta X, it DOES become infinitely better at estimating the slope.
6.5
Well crafted!
9
Very fascinating and well-paced. I appreciate how accessible this is to non-mathematicians, given the pre-requisites mentioned. My only feedback/note is one of minor detail. Before you expound upon the partial derivative of d_sub(xx)u(x,t) ~= blob, the preceding statement needs a "be" between "should," and "quite." I hope you continue coding this up and share more next year!