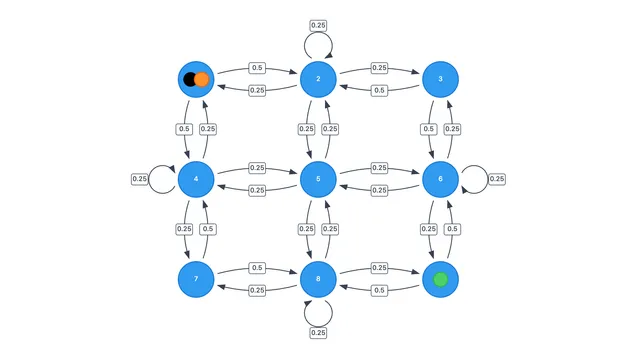
When do Markov chains converge?
Audience: undergraduate
Tags: probabilityapplied-probabilitymarkov-chainsstochastic-processesapplied-stochastic-processes
The goal of this post is to present some standard Markov chain concepts (specifically, the Fundamental Theorem of Markov Chains) but make them genuinely intuitive through interactive visualizations that let you explore the ideas hands-on. This post is written for undergraduates who have some probability background. You'll get the most out of this if you're familiar with basic Markov chain concepts (states, transition matrices, etc), but even if you're not, the interactive elements should help fill in gaps, and a quick Google search or ChatGPT query can clarify anything unfamiliar.
Analytics
Comments
This was the best entry I’ve seen yet, it took me a while to read this and understand the math even though I thought I knew most of the basics, but it was super worthwhile. I loved it! Please write more articles like this!
The demos and “try yourself” portion was very effective, congrats!
Cool visualisations, but maybe they could be distilled a bit. Very worthwhile content.
This is a great article! Very clear explanation, and nice interactive widgets.
My only note is that who the target audience is feels a little inconsistent for a brief moment at the beginning: on the one hand you suggest people should already know some things about Markov chains, and on the other you give a very basic example to illustrate the Law of Large Numbers; it’s hard to think of who would be in the first category but still benefit from this example.
But otherwise, very nice work. On the rubric, the clarity and novelty are great. I do think the motivation could be improved a bit, and you could do that by starting with a case or two where this material really clarifies what’s going on, or maybe exploring the history in more detail (which was covered in a recent Veritasium video). That would help with memorability too, although your visualizations are going a long way on that count.
Thanks for writing a comprehensive treatise, with examples, regarding Markov Chain convergence, as well as building interactive visualizations to supplement the article. I’ve bookmarked it so I can further study it after SoME scoring ends. I’m wondering if you’ve heard of the paper, “THE $25,000,000,000∗ EIGENVECTOR THE LINEAR ALGEBRA BEHIND GOOGLE” (link: https://www.rose-hulman.edu/~bryan/googleFinalVersionFixed.pdf) and can write another blog explaining how the embedded FTMC and SLLM apply to PageRank. I’ve set you Ranking score as an average of these individual scores: Motivation: 9 Clarity: 8 Novelty: 7 Memorability: 8.5
The visuals for representing state transitions are useful. The maths however, has inconsistent styles which causes some confusing. i.e. x=xP, it was never clearly specified that x is a vector, or P is a matrix. But also, P[x=i] as … probability? and reuses j as both a state or an index when it’s a subscript. Would be much easier to follow if the notation is clearly explained.
Really really nice simulations, really interesting topic, and perfectly in the context of SOME! I removed a point from the maximal grade, as I think that it lacks of a bit of “real world” introduction or motivation : think of physics, biology, … as it is really easy to do that with this topic, and that would really make your presentation perfect. Still, many thanks for this really nice article!!