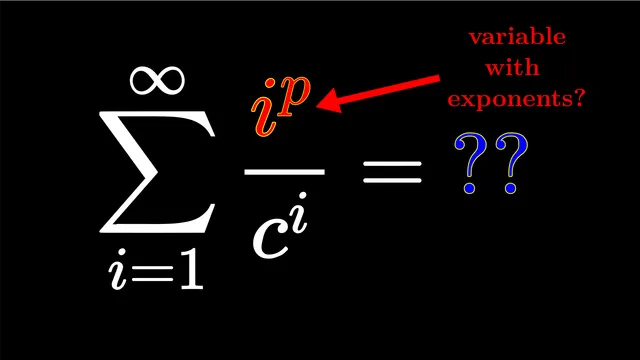Summer of Math Exposition

Could have done with an introduction to tie everything together and introduce the topic. Terms and and definitions are well described. Examples are used well to explain the topics. Extra proofs and asides such as the connection to a geometric distribution are a nice extra. Breaking the article up into sections made it easy to read and follow. The article was well referenced and gives extra reading for those curious. I liked the article ending on a link to Dirichlet series and an unsolved problem to keep the reader thinking. The overall layout was very clear making it easier to follow the content. The topic chosen has general interest and was well chosen to allow people of all abilities to understand. Overall a really good article

Great job with expounding upon the ever-present geometric series as well as its applications, and providing papers that accompany your tutorial. This could be part of a series (no pun intended), of work that dives into lorenz attractors, or some intro fractal sets!

It does not offer any intuitive explanations or visualizations for the sum of the series involved.

Level 0 through level P was super clear. I loved it!

love how the article presents the concept in a clean way and builds from a simple to a more complex format of the problem still i think the explainer lacks that aha moment - something that makes you smile at the end and think "that is neat!"

While the presentation is clear and concise, I didn't feel that this article added anything new or provided any new perspective about summing series that doesn't already exist in standard literature.

This was a very fun exploration beyond something that is taught in every introductory analysis class, I can imagine a student who has taken this class and found it interesting will really enjoy this article. You have a cool blog :)

I like the presentation and clear explanations. Hiding away the proofs etc. is a nice touch. This reminds me of a Mathologer video that also computed a sequence of sums in terms of previous results.

A wonderful explanation of generalising such a simple sum. I really appreciate the heavy use of references.

It's always lovely to see generalisations at play. It was an enjoying read. thanks!

I like how the series were gradually built towards more complexity, guiding the reader along. It would have been nice to have seen some concrete, real-world, examples in action/more depth (e.g., of the combinatoric variety mentioned).

some part was unclear...mainly the last one...

_real_m got me good. Great explainer that really only lacks in the novelty arena.