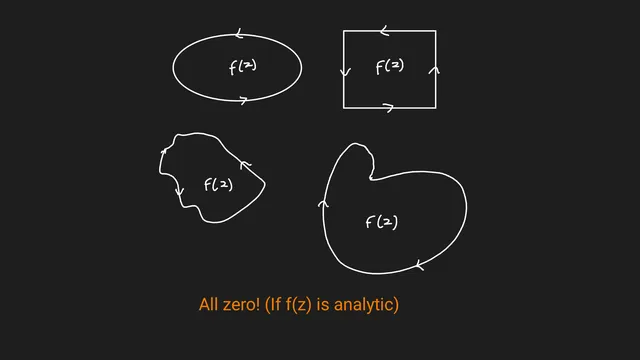
A proof of the Cauchy-Goursat theorem
This expository article presents a proof of the Cauchy-Goursat theorem along with the motivations for it. I would have liked to have some handout like this when I was taking a complex analysis course, so that is what I have attempted to make with this article. The article was written with a goal to help the reader prove the result on their own. It is aimed at an undergraduate student and assumes familiarity with some basic concepts in complex analysis.
Analytics
Comments
7.1
Nice proof - this is definitely one of my favourite theorems in complex analysis! I think maybe the example with Corra at the start wasn’t very helpful, since you didn’t really return to it or give any motivation for why the energy could be negative? Maybe an example with, like, magnetic fields and wires could’ve helped, I’m not sure. Also think there’s a small typo - the energy function should be from C to C?
I do like how you generalised it to arbitrary contours - that’s definitely something I hadn’t seen in my complex analysis class, at least not with this proof technique :)
6.2
[minor typographical feedback] While I liked the presentation, perhaps white serif text on black is a little bit hard to read. It's clearer to use sans-serif text when writing white-on-black. I thought the smiley instead of a QED symbol at the end of the proof was cute. :-)
2.6
This ranks fairly low on the motivation and novelty scales. It was clear and well thought out, but a proof will always have a hard time standing out in a field of exposition.
9
This paper was a lively, honest and gentle walk through what initially appears as monumental task to prove, "The Cauchy-Goursat Theorem." In my opinion, you've removed the immediate barriers which may trouble those who read math with regard to unfamiliar definitions. (E.g. simple closed contour). I appreciated how things were color/colour-coded when partitioning the triangles for the C-G theorem for triangles. This will take some bandwidth, but it'd be really neat to see the lattice structure placed in a simple closed contour, triangles appended, and the general simple closed contour, "absorbed." This paper was clear so that I was able to visualize your work in this manner, thank you!
1.2
The analogy given in the start of the article is bad. OK, I can imagine a vehicle going along a path and using up some fuel. But then, it turns out that it can actually produce fuel. (I could imagine that it has some wind turbine or power generator to produce energy when going downwards, but that is distant enough from the intuition you give to make the immersion break).
On top of that, there are errors (wrong notation for the set of complex numbers in (2) which I see that the Author already acknowledges, in (3) and the statement that "energy can be negative, positive or zero", while the contour integral is a complex number in general).
This is aimed at a very specific audience (people who know what a countour integral -- a rather unintuitive concept -- is but they have not yet understood the Cauchy-Gorsat theorem). It is long since I took my complex analysis course, but I do not feel that theorem is especially unintuitive.
2.9
Even though I am not an expert in math, I followed the demonstration of the theorem and technically it seems ok, but this is not a presentation ... The author more or less took a theorem from a book and is trying to claim that he had done some work to explain it... In my opinbion that's not true... no aditional work is done here... This presentation is not a good one...
5.9
Explains the concepts well. Its a little bit on the more technical side.