Ellipse Theorems – Defining Perimeters and Reshaping Geometry
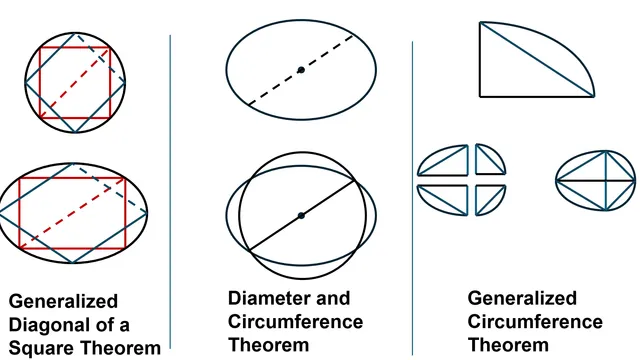
This Paper defines three new ellipse theorems. The three theorems are as follows: • The Generalized Diagonal of a Square Theorem • The Diameter and Circumference Theorem • The Generalized Circumference (round shapes) Theorem The implications of these theorems are as follows: • An exact ellipse circumference equation (closed form) • A unification of the ellipse and circle equations for circumference and area • A new group of rounds shapes with defined circumference and area equations This is a link to the accompanying Desmos Graph - https://www.desmos.com/calculator/bkr35tpff9 Everything explained in the paper is interactively demonstrated in the graph.
Analytics
Comments
1
Unfortunately, this proof is incorrect. The approximation for the circumference of an ellipse is not in fact exact, and this can be proven by using calculus and integrating the parametric equations to find the true perimeter. Additionally, there are many other approximations for the perimeter of an ellipse, some of which were given by Ramanujan. If simply multiplying the diameter by pi always gave an exact solution, these approximations would not be needed. The proof presented in the paper is fallacious because even with the demonstration of Thales' theorem, it never actually proves that the circumferences of several ellipses and the circle with a given diameter are equal.