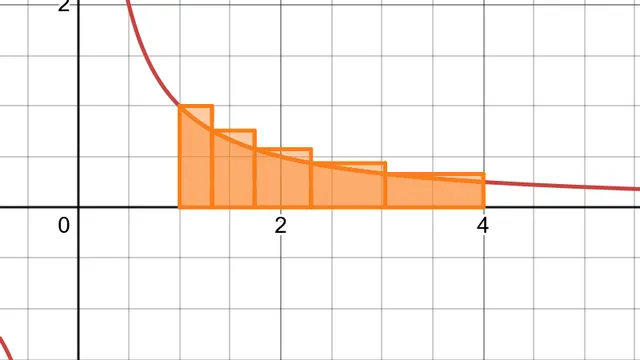
The Quadrature of the Hyperbola
Audience: high-schoolundergraduate
Tags: calculuslimitsintegrationdifferentiationnatural-logarithm
An article about integrating the function y = 1/x from first principles. 30 pages. Aims to give an intuitive and engaging explanation of why the natural logarithm is the measure of the curvilinear area underneath a hyperbola, with plenty of diagrams. Presupposes knowledge of arithmetic, algebra, and coordinate geometry; delves into elementary calculus.
Analytics
Comments
Really a great introduction to integration, and the ideas behind calculus was shown in clear an natural way.
Motivation
The motivation for why this is needed/ why I should care pretty lacking.
Clarity
This article does a great job clarify, there was no point where I was confused or had to search something up, this does mean the article was a bit too long for my taste, but I think it would make it easy for anyone to understand this article
Novelty
The first part wasn’t really something special, however using the geometric series to partition the hyperbola was something I never seen before and builds a better connect between the harmoic and the logarithm VERY NICE!
Memorablity
Due to the length of the whole article and how much information is in it I would say that it suffers a bit from a memorablity stand point however, Lots of the ideas could be easily understood and can have a learn a lot from this article
This is an interesting and well written article. The topic of quadrature, limits, derivates, etc is not particularly novel and there are now many great resources on the internet for it, but this is the first one I have seen focused on the hyperbola in particular and I think that made it more interesting. Saying that, I don’t think I would recommend this article to a student not familiar with the basics of calculus, limits, and quadrature already, so all the time spent explaining those ideas could probably be trimmed (making the whole thing shorter, which would also be nice—students will usually not read really long articles unless they are very engaged the entire way through). I would probably recommend them something simpler and then possibly use this to (in part) introduce the logarithm function. On a different note, using geometric quadrature was new to me and I thought it was neat! Overall, nice work!
If I were learning calculus again, I would like more detail on why the actual integral is the natural log of the magnitude of x.
Very clear and intuitive explanations. I personally feel the article attempts to appeal to cover too much ground, e.g. going through logarithm, derivative and integration first principles.
Somewhat verbose. The reveal in act four seems too forced and the exposition about the properties of the exponential and logarithms is unnecessary.
I realize I’m not the target for this, but mid way through it I was just thinking it felt unnecessarily long, like the same concepts being repeated over again. It also didn’t help that you start focusing on geometric intuition but we end up with too many mathematical expressions and it feels more like plain algebra than geometry. Surely there must be a shorter and more beautiful way to introduce the natural logarithm? Maybe I got the false impression that the aim of the article was to show that area is the natural logarithm much more than introducing calculus. If calculus was the main aim, then I would still say it’s unnecessarily long, and it suffices to use the traditional arithmetic sequence rectangle approximation.
I also had one specific doubt on this part:
For example, consider the parabola, . A straight line, whose slope always stays the same, has the equation , where is a constant defining the slope. The parabola’s equation can be written as . This suggests that its slope should increase as increases, and decrease as decreases: it should depend linearly on .
Why do we conclude that it should depend linearly on ? Assuming we don’t know anything about derivatives. For me it’s unclear.