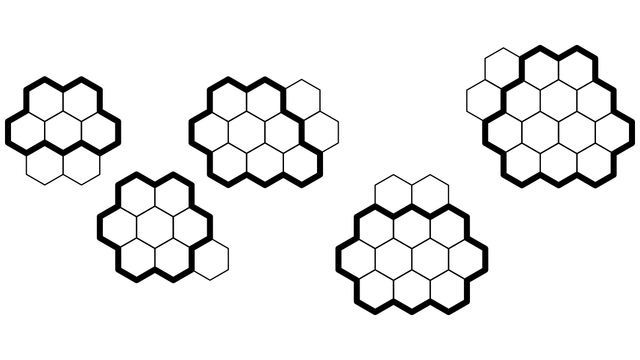
Pellagons
Exploring the integer pattern that emerges from a set of simple construction rules on a hex grid.
Analytics
Comments
6.5
Motivation - Better than most. I enjoy these sorts of OEIS sequences that are easy to explain but yield deeper mysteries.
Clarity - About the same. Explanations could be improved to be more "professional" (footnotes are fine, what I mean is the overall direction of the submission), and it would seem that there are some redundant parts. But overall, the explanations are understandable and fundamental to viewers with minimal background.
Novelty - Outstanding. Clearly, as this sequence is not in the OEIS, it is highly novel
Memorability - Not as good. Unfortunately, there doesn't seem to have been any linkages to other sequences, or finding any closed form analytical solutions for the new sequence, or even identifications of things like "are there infinitely many terms", etc
3.1
The introduction didn't lured me in.
The language seems hard. Need simple explanations.
6.6
Very interesting topic with how, "Hexagons are the Bestagons." (thanks for the video reference!) I think this article is very close to approaching a full exposition of the Pellagons/Pell Tiles topic. I recommend writing up a brief summary of the Pell Tiles post on the same page. This is because I found myself clicking to many of the citations, was led to YouTube, then recognized I needed to read the Pell Tiles previous post in order to understand the main point of Pellagons. I'd also recommend defining some concepts that build up to Pellagons: convex and convexity properties, maybe some simple connectedness? Then it was a strong leap for man to go into the bounding bags section. Thus, I'm left to understand if I fully understand the definition of Pellagons, Pell Tiles, and well, I'll keep trying!
5.1
Fun article!
3
The first animation appears to not work and the author assumes the reader to have read their earlier post, thus making the entry less approachable than I would have hoped.
5.5
I really don't like having popups appear when I'm trying to read things. If possible, you should have turned that off. I didn't mark the maths score down for it, but I normally blacklist any web site that spews a popup in front of me, even if it's just a 'please subscribe'. It's kinda rude, and as web sites are ten thousand a penny I see no reason ever to tolerate it. So I don't, I'm afraid.
On the article itself, it loses a little on Motivation, and a little more on Clarity (it feels like there's a missing sentence somewhere that explains things, and without it I'm unsure I'm fully following the thread you're trying to explore.) Plus for Novelty and Memorability though. When drawing ever-growing chains of hexagons around a central point, the sixth one is sort of C-shaped. Yes, and? And thereafter you generate six-sided shapes which tend to be a bit irregular. Yes, and? And here's the OEIS sequence. O-kay. I feel a little uncomfortable, like I've come in 60 seconds late to a graphics lecture and just missed the introduction. (I hope you know the feeling I mean.) If that's all you were covering, then fine, I'm good. But if there was more, I've missed it.
6
Interesting! Good luck with undergrad, keep it up!