How Long Does a Bingo Game Last on Average?
Audience: high-schoolundergraduate
Tags: probabilitystatisticssimulationgamesdata-analysisrandom-variables
Simulations of probabilistic games are important stepping stones in statistics and computer science. This submission explores simulations through asking questions about the game Bingo. The submission will walk through the ideas around the simulation, including classic chestnuts like the law of large numbers and trend analysis. One place where I feel this differentiates itself is incorporating the tools of curve fitting to finding a final solution to the problem. This type of problem is usually explored at the end of high school or the beginning of college and can be used after understanding simulations of simpler events like dice rolls but before studying non-probablistic games like checkers or chess. While this is not a lesson plan, per say, I enjoy writing in a conversational tone that may allow this to be used as an outline for a talk to an audience familiar with some of the background information.
Analytics
Comments
Very interesting! I’ve wondered this question, too, and it was nice to see your process for answering it.
Explanatory
Really well written article, and i like that you approached it without any formal or high level math. This makes it really accessible.
One things I’m wondering is could you not simulate this with only one array for the board? Because each number is equally likely to be drawn, it does not matter what the numbers are except that a number can’t be drawn twice. As such, the indices into the array (with an offset to account for the free space) can be there “board numbers”, and the simulation should be the same. I’m curious whether I’m correct on this.
I really enjoyed how simple and informative it was. An interesting question, solved in a classic way; amazing! Would have loved if this were a little longer, maybe an interactive bingo window if possible, or talking about the near misses a bit more that are referenced at the end. What if the bingo grid was bigger?
Something interactive would be great. I think this can be relatively easy to do with ipywidgets and sliders, for example, showing the distribution versus number of trials and convergence to the average.
Pretty fire
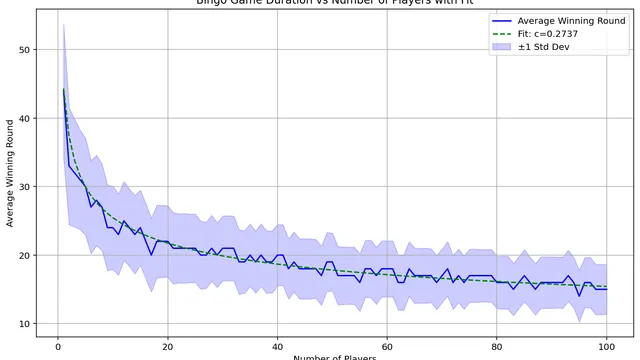
- surprising that the decay exponent is 0.2737 and not a simple number like 1 or 0.5
- good job observing that the curve should have asymptotes at x=0 and y=4
- you can consider graphing x vs. y-4 on a log-log plot; this should transform the trend to a straight line and make it easier to find the decay exponent
This written explanation of how mathematics is connected to the game of bingo is an excellent example of an investigation into a simple topic being used to demonstrate multiple areas of maths. It uses probability theory and graph fitting very well.
However one criticism is that is does not display a bingo machine or a bingo card which the reader may be totally unfamiliar with. Since this contest is aimed at engaging school age learners such simple graphics would definitely add to the presentation. Even if they may be considered non academic.