Feedback – SoME

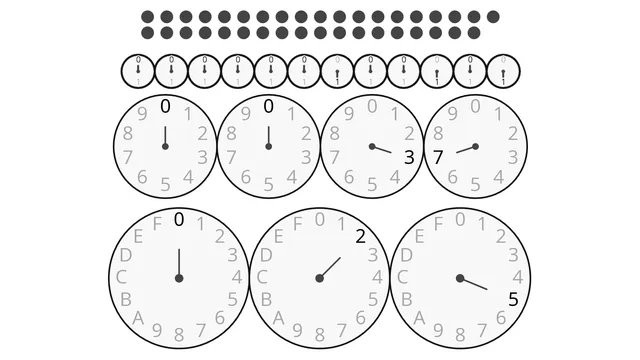
If you can read clocks, you can understand binary and hexademical numbers

Audience:

Tags: binary-numbershexadecimal-numbersnumber-basespositional-notation

I tried to come up with a more intuitive explanation for positional notation, using analog clocks as substitutes for the digits. The visualizations of article are interactive, so you can play around to see the values change on the clock faces themselves, which hopefully helps with giving people a feeling for the system. Along the way I share some musings on positional notation being a form of data compression, and how this data compression also allows for faster calculations of bigger numbers. Even if done by hand by humans! While I wrote the interactive notebook with a teenage-or-older audience in mind, I suspect the visualization and core idea for the explanation itself could work for elementary school children too. My motivation behind it was my own memory of feeling incredibly frustrated with how binary numbers, hexadecimal numbers and positional notation in general was explained to me as an undergraduate. Even more so after I understood them and realized that the whole idea was much simpler than the explanations made it appear.

Analytics

6.8 Overall score*

14 Rank

12 Votes

6 Comments

Comments

Quite a good analogy for different base systems, with good visualizations. The dots could also have been used to convey the idea that “the place values represent different powers of the base” like the clocks do.

I like your visuals.

I created something similar a few years ago for teaching how to read clocks. (Our JavaScript code is quite similar.) I made it so the hands of the clock can be moved by dragging them. This feature on a phone touch screen seems to make it very engaging to my students, they ask after I teach time if they can play with the clocks, and continue to check their answers. If your interested (perhaps for teaching your daughter how to read analog clocks) scroll to the bottom of this page: https://mathsfromnothing.au/time/

8.5

Solid writing and really nice visuals. It’s a great alternative to thinking about these base-n systems and a great explanation. I love the interactivity of the clocks too!

6.7

I really enjoyed reading your post! The clocks’ running is pretty fun and satisfying to watch. Your post provides a really intuitive way to understand different number systems. The interactive is simple, yet adds to the clarity of your explanation. However, I met a little bit of confusion when you do the arithmetic part to translate “37” to an octal or hexadecimal number system. Maybe you could give a general formula to translate from normal number system to others. Moreover, the motivation of the post is data compression, but I only figure this out in the middle of the post. They should be clear at the start.

Overall, this is a really good post and makes me interested! Keep up the good work!

6.3

Nice widgets and explanations - one nitpick is that the sliders make the clocks move so fast that it is hard to deduce anything.

I think it would be great to show an actual clock, with the small hand sweeping twelve hours and the large hand sweeping sixty minutes, to ground this idea—it’s implicit in the title and explained well in the article, but showing people the familiar example roots the explanation in experience!