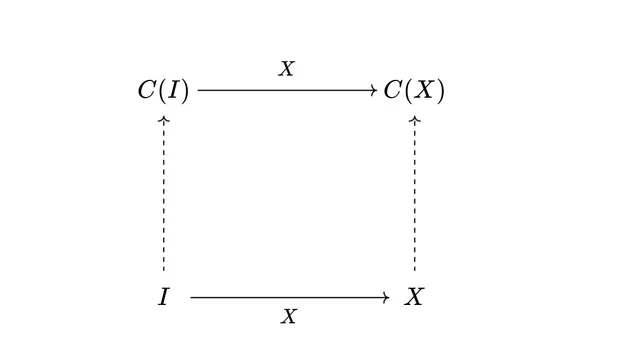Summer of Math Exposition

I really liked the conversational tone of the article, and it's clear the author knows their stuff. Where it lost me was "covariance" and "contravariance". I never got a sense of what those words really, truly mean, and I think the diagrams made things more confusing for me, not less. "The hard part was more creating useful definitions, covariance and contravariance, that made the problem simple and transparent - which is often what category theory feels like." Unfortunately, adding the category-theoretic machinery did not make this problem feel simple or transparent to me - I think it would've been much easier for me to attack this question purely within linear algebra land, even after reading the article.

I think this is a great introduction to category theory. Good job!

You have the tone of a strong educator, and did well building from first principles. A little weak on the motivation/novelty but I enjoyed it overall. (Thanks for sharing quiver!)

I liked the numerous examples to explain covariance and contravariance, and this explained was a way to think I haven't seen before. It would be nice if the article gave a small introduction to how this is formalized in category theory

I’m biased, but this is a perfect explanation of something I’ve already seen and understood thoroughly.I can’t tell how a beginner would take it. Maybe they would care if they heard of category theory. Maybe they would need to see one more example of something with potentially many degrees of freedom (doing a column op) being determined fully by something with only one (determined by left mult by some unique matrix), AND that it’s determined by what happens at the identity. Every group G (or even monoid) can be regarded as a category BG with one object, and whose homset under the composition structure is just your initial group G (basically, a monoid IS a one object category, and a group IS a one object category with every morphism invertible). Then a functor from BG into some category, like SET, has all the same info as a particular G-Set. So the category of G-Sets and action preserving functions is exactly [BG,SET]. Here’s Yoneda applied to that: For an arbitrary set with a group action, X, how do you determine an action preserving function f from G to X, where G is taken to be its own G-set under left multiplication (ie, left regular representation)? Super easy. For an arbitrary g in G, you need to define f(g) in X. But f preserves the action, which is just group mult in the domain, and a given in the codomain, and g can be written as g x 1, so we have f(g)=f(g x 1) = g x f(1). There, an action preserving function from G to X is literally directly determined by where 1 goes. This is sort of silly as a stand along fact, but I think it illustrates the idea nicely, and gives more evidence that this idea with elementary matrices fits into something bigger. Oh, same for poset categories. If every homset had at most 1 element, things simplify in a different way, and you end up with a statement something like “x=y” iff “for all z, z<=x iff z<=y”. Which is also a nice observation by itself, but nothing too crazy. This is explained further in Riehl, and idk if the first one was from Riehl or Leinster, but the point is: showing the lemma reduces to something reasonable in these greatly simplified situation (one object category, poset category) can give someone a sense for generally HOW does the Yoneda lemma say that some complicated stuff is totally determined by very little, and that stuff is determined by what happens to the identity. I probably wouldn’t have cared if elementary matrices were the only example I knew. I would need just a little more evidence that it extends into other situations, and might look very different in those! Hope this helps, I’m glad someone made a post about this!

Great article! Helps me understand how matrix multiplication covariantly relates to column operations Some content in paragraphs felt a bit roundabout. Sometimes words like "just" or "clearly" described non-obvious things. Took a moment to parse through the concepts and notations to understand why it was marked as clear A bit unclear which parts of transpose and row operations are contravariant Love the distinction between row/column operations and matrix multiplication Overall progression felt like an interesting journey!

Very detailed piece about Fundamental Linear Algebra. A lot of work went into this & it was well written. Good job!

Nice article! I like your unorthodox way of presenting category theory concepts. I'd love to see how this relates to the Yoneda lemma in more detail.

In the contravariance section, perhaps you could label the input and output domains? (label the bottom of the cm and meter example "unit" and the top "measurement") In the matrices section, maybe specify that the lambdas are arbitrary constants (immediately--even before the sentence "If we were swapping..."). Thanks so much for the intro to category theory! It was awesome.

It's not clear to me why the main premise of this article is any different than 3b1b's explanation that the columns of a linear transformation matrix indicate where the basis vectors are mapped to. I admit I know little about category theory, but it seems overpowered and perhaps too complicated for explaining matrix multiplication.

I was enormously distracted by the side link to galactic algorithms - thanks for that link

Great job making it look so clean and using fruit as part of the example to make it overall seem less complicated. Little things like that I just think add up.

Excellent, really found the right sport of depth and approachability!

Very cool, nice result and satisfying deductions. I feel like it started to drag a bit with all the formulas and proofs but that might just be my attention span. Would've liked more explanation of what category theory is. And what that lemma is exactly since the proof is about matrices and I'm not sure how that relates to a general result. A bit of required knowledge that would've been good to explain or maybe reduce the jargon. Feel like more definitions might help instead of only examples like I get the rough idea of what covariance is about but what is it exactly?

Nice introduction to category theory and how contravariance and covariance works as this topic is not the most easiest to explain with lots of abstraction. I think there is a good balance of using real life examples to make the relations a bit more digestible. I'd like a bit more of a concrete example with matrices with some numbers to help to improve and let us visualize the operations a bit more.