Feedback – SoME

Introduction to Solving Ordinary Differential Equations Numerically

Audience:

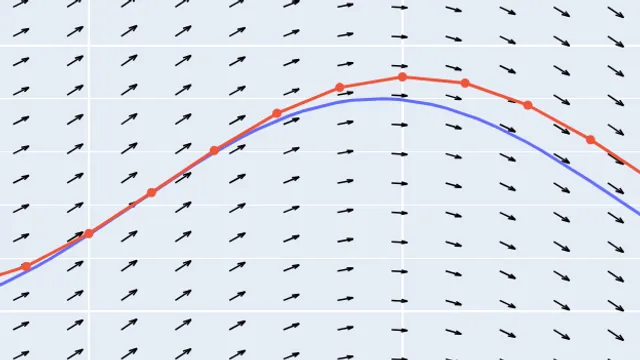
This is an interactive notebook that provides an introduction to solving ordinary differential equations (ODEs) numerically. We first discuss how ODEs can help us predict the future and how they are defined. After that we look into slope fields to get a qualitative idea on how the solution to the ODE behaves. From there, we will develop the Euler method for solving ODEs numerically and look at three different interpretations of Euler's method, which give us insight into how to design the parameters and develop improved methods. The intended audience is everyone who wants to get an intuition on how ODEs are solved numerically. The entry is probably suitable for high school and undergraduate students.

Analytics

7.5 Overall score*

6 Rank

11 Votes

7 Comments

Comments

5.9

I would have loved to have seen some more exploration of how slope fields are related to phase spaces and how they can help visualise ODEs

8.6

This was an outstanding piece! I really liked your analogy when explaining Euler’s method. The exposition was clear and follow able for anyone with a small background in calculus. You clearly motivated the study of ODEs (e.g., it use in various different fields), and presented several tangible examples. While the presentation is not entirely novel (as expected for a discussion of ODEs), it was very fresh and intuitive. Keep up the great job!

I like your presentation of the different methods of obtaining Euler’s method. However, I think there are two points that have been missed from an introduction to solving ODEs numerically:

You need to let the student know the computer should do the mindless calculations, doing numerical calculations by hand is a great way to make a student hate numerical methods.
You typically do not know what the error is, therefore you typically use two methods, with the difference an estimate of the error, then adjust the step size to be as large as possible without exceeding your acceptable error tolerance.

8.1

The sliders are a very nice addition

6.7

Very clean layout. I enjoyed the part about solving ODEs a lot, but the beginning motivation could be improved.

7.7

The interactivity allows for people to play around to see how the values affect the output. It was clear about how to interpret these graphs. And useful describing how things worked. Explanation is also worded in a digestible chunks.

7.5

Detailed visual displays, but where is the final comparison of the number of function evaluations between Euler’s method and Heun’s method.