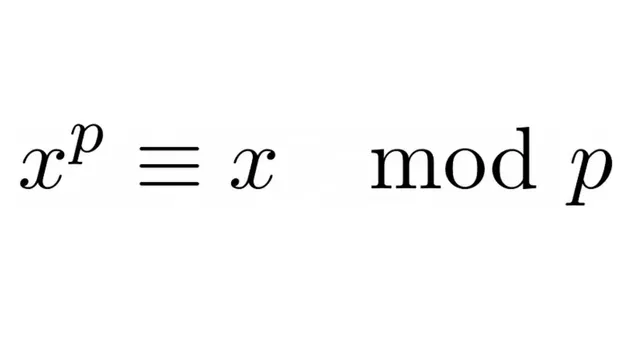Summer of Math Exposition

Concise yet very interesting and accessible.

A few typos: In “what I believe is the most beautiful little theorems in maths”, either “theorems” should be “theorem”, or else something like “one of” should be inserted between “is” and “the”. “my” should be “by” in “we can multiply numbers my other numbers” “with” should be “when” in “which does not happen with p is not a prime”

This is one of those explanations where I already knew each individual piece you were using, but it's still a lovely construction when you put it all together. (And any reference to Fermat's Little Theorem always makes me happy, because as a teenager, I was fascinated by something that I was unable to prove, but unable to disprove - and when I got a chance to ask a math newsgroup about it, I learned that what I'd been exploring was a derivation of Fermat's work. So there's a bit of personal nostalgia for me.)

I think the section with the substitution of u-1 for x lost me a bit, particularly the second iteration. Otherwise, this was an interesting topic, and it's nice to see a novel approach. Thank you!

Thank you for your article! Borrowing from poetry in the form of a simile, I finished reading your article and found it to be like a brisk walk in a number theory park. The survey regarding modular arithmetric and its relations with Fermat's Little Theorem/Little Theorem of Fermat (LToF) were thorough yet concise. That being said, I'd work on the build up of the sequence from the binomial theorem, into the freshmen's dream, to modular arithmetic, and to LToF using the concept of the freshman's dream. The concepts explained are clear, I most especially appreciated the analogy of seeing mod arithmetic as a clock. Although I must say, the conclusion left me with piece-wise information, and I've arrived that it's my job to assemble the puzzle pieces to make a continuous whole. If this is the intent, then great! I hope you include this in the conclusion summary to "make it obvious," for those who are reading. If this is not the intent, please know you still gave wonderful insights to arrive at a proof to show LToF by way of the freshman's dream and an understanding of mod arithmetric.

Same topic as Numberphile, but the last part was interesting

I like the relaxed approach to the topic. The introduction is very catchy and it will generate interest in anyone that had to deal with powers of sums. A "real" motivation (in the sense of applications) given in the beginning would be nice to have.

Cute, short. Was this partly inspired by the recent Numberphile Freshman's Dream video?

Cool!

What a great approach!

What a surprising result from something so simple and I'm delighted to have seen this today. It may be a bit difficult for someone not too familiar with more advanced mathematics to follow as I'm not sure everyone will be familiar with what primes are, so we could just leave it as a smaller elegant proof. There are some spelling mistakes, but these are minor ones.