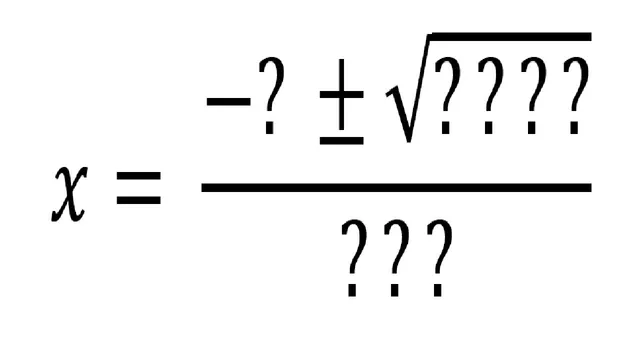Summer of Math Exposition

Great idea, executed well. I loved the addition of a storyline into this article; it became alive, I could see myself going through this process. Also an idea I'd never seen before, to use checking your units to figure out the quadratic formula. Really well done!

The setting and the theme were very interesting. The main thing that bothered me was the complexity of checking the units. Article describes multiple ways to interpret units in a calculation, while never explaining only the algotitem in it's fullest. There are also simpler ways to do unit analysis, which left me pondering why the extra complexity.

Cute story! And a nice application of dimensional analysis outside its usual realm (physics).

Was a good explaination, but felt anticlimatic as someone with knowledge of the quadratic formula would be able to pick the right answer out of the list and skim over the rest of the article

This made me smile. A little modern math parable. And, a real-world example, I was talking to some online friends and they were complaining about have had had to learn Pythagorus but never having had to use it since school, and bemoaning the wasted effort. I felt honour bound to put my hand up and say, 'I've had to use it.' Pythagorus-users and quadratic formula-users may be in a minority, but there are a scattering of us out there.

Units are physics topic, not mathematics.

I actually did not know that after ruling out some wrong identities via an assignment of dimensions, it is still possible to rule out other wrong identities by making a different dimensional assignment. So I was pleasantly surprised by the fact. However, this brief article doesn't do justice to the topic. The short story feels like a simple introduction to a deeper analysis of the method of dimensional assignment. One thing I was left wondering is wether or not the "assignment of dimensions" can be achieved in a purely mathematical framework, without invoking physical units, and without talking about "length vs area vs volume" in a loose way. The first thing that could have been done is more examples: - An example in which one may want to assign different units to the variables, instead of just a single unit and its powers. (Like using "time" and "length" (and their combinations)). - Maybe an example with "special" functions, like e^x: is it possible to assign a unit to x, or does it have to be dimensionless? In Physics probably it can't have a unit, but maybe the concept of units can be generalised mathematically to allow it. In any case a mention of the impossibility/possibility would have been good. Another thing that could have made for a better article is that of identifying the problem. I would call the problem "Dimensional satisfiability", and I would define it as (loosely): given two sets (finite, or also infinite) of equalities in some variables, determine if every dimensional assignment of the variables that satisfies the first set of equalities also satisfies the second set. (A variant would be determining the maximal subset of the second set that is always satisfied). And I would discuss the following points: - For which types of equalities does it make sense to define it? Only polynomials in multiple variables, with not-necessarily-integer powers? - How to phrase the problem in a more rigorous mathematical way? I think maybe by asking whether it is possible to define a map f from the set of variables to she set of monomials in the units such that there exists a map g from the set of given polynomials and their "subpolynomials" to the set of monomials in the units that satisfies g(a)=f(a) for every variable a, and g(p/q)=g(p)/g(q) for every p,q, and g(p+q)=g(p)=g(q) for every p,q in dom(g) s.t. p+q is non zero and is in dom(g). ((This is just a very rought definition I came up with to give an example; it may also need to be adjusted as I am not too confident)) - Is the problem equivalent to some other known problem? - Is it always possible solve the problem? If so, how? - Can it be done algorithmically? If so, with what computational complexity? Then the article should dedicate some time to answering questions like: - Is there a "universal" assignment for every pair of sets of equalities? Meaning an assignment of dimensions to the variables, satisfying the first set, such that for every assignment that satisfies the first set, every non-satisfied equality of the second set is also not satisfied by the universal assignment. In other words: an assignment that satisfies the first set and that identifies all of the equalities of the second set that are not compatible with the first set. - How many different assignments does one need in order to solve a dimensional satisfiability problem? And for the variant of the problem? - How many different units does one need to use? - Is it possible to solve the problem (or its variant) by making multiple assignments, each using just one unit (and its powers)? - Is it possible to solve the problem (or its variant) in a unique assignment (with possibly multiple units)? - How to minimise a certain combination of number of assignment and maximum number of units used in single assignment? Then there should be further comments on topics like: - Are there alternative ways of doing the same thing that dimensional assignment achieves? - are there any applications of the method of dimensional assignment? Does it have any actual uses (in pure mathematics, or in an applied field)? Finally, one thing that this article lacked and would have been quite valuable, are references for further reading on the topic. In conclusion, the topic is really cool, but the article does not develop the theory in any way, and basically every possible quesiton the reader might ask is left unanswered, nor acknowledged.

Bonus points for earnestness. I’ll bet this would be useful for students who are first learning the quadratic formula.

I hope this well-written article will be iterated upon to produce a video entry that shows a "Jeopardy"-like scene where Anna and her inner problemer solver character (like Joy of InsideOut) journey over to geometry land and win th prize.

Great job! However it seems there's still room for more math.

I really love the mix of narrative and dimensional analysis. Great work!

It was a fun to read the article. Gives good insight.

I enjoy reading it. In fact, I've a similar observation about this (in)famous formula too, however, I never delve into it this deep. Suggestion: - There's too many choices, (A)--(H), that's quite tedious to read them all (I didn't read it). You could just go for 4 standard choices (A)--(D). Since you can't enumerate every possible combination anyway (and if you're really enumerate them all, some of them will agree with your "unit" method, especially that something something inside the square root.)

While there is lots of focus on dimensional analysis in physics, it is rarely mentioned that it can be used in purely mathematical contexts too. This very good submission nicely fills this gap. Incidentally, MY physics teacher has been repetitively saying the following: do not learn formulas, instead, learn where they come from. I think this has influenced me a lot. I am of a strong opinion that is pointless to memorize this formula and instead learn how to go without it. (This is of course not a critique of this submission which also mentions this, rather of the way that math is usually taught...)