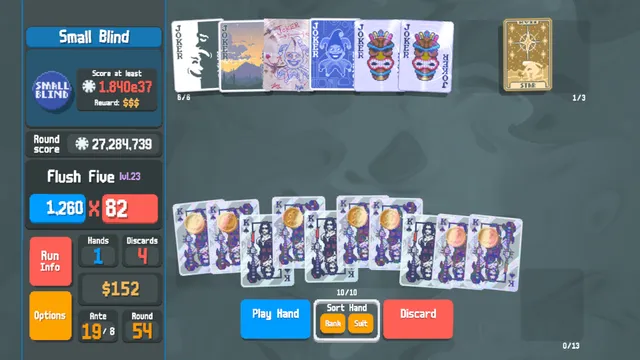
Using Geometry, Quadratic Functions, and Calculus to Prove Why You Should Balance Scoring & Retrigger Effects In Balatro
Audience: high-schoolundergraduatemiddle-school
Tags: gaming
A look at a specific behavior in the video game Balatro, including its mathematical properties, and a proof on how to get the best score using this behavior.
Analytics
Comments
I think you have a typo in your definitions:
“If t is the number of triggers and s is the number of scoring effects, area (p) and perimeter (t) can be represented by the following equations:” as t is defined as both the number of triggers and the perimeter, and you write a=ts for the area below.
Nice to see a simple application of recognizing maximizing the score corresponds maximizing area.
The card game was interesting and the writer did a good job explaining it, as someone who had never heard of it before. They provided clear motivation for creating the maths puzzle, and the link with geometry was fun. The mathematical process was easy to follow and concise. Overall, a very solid article.
i loved the game and even more the explanation given here
Great attention to style, the only downside is that you may need to be familiar with the game to fully appreciate what’s happening here.
I love some game optimization. As a teaching tool, this suffers a little bit. I think you could have done a little more to ease the reader into the example. Perhaps more screenshots with less going on at the start and using highlights to circle what you’re talking about as you’re talking about it. Short of that, figure numbers. This is a really nice use of a classic maximization of area and minimization of parameter problem. I can imagine a world where this is a really interesting article, but it needs more work. It may also help to provide some introduction to the math as you describe the game. Trying to mix in multipliers while still describing the game got me a little lost.
As an aside; really nice formatting and thematically matched to the game you’re discussing, which was nice.
Very unique - some visuals in the “quadratic functions and calculus” section would be nice.
I enjoyed reviewing your themed article with a themed website. That being said, I’ll probably never play Balatro yet totally appreciated how you noticed patterns and made geometric sense of it through modeling via quadratic equations. The Ranking score I’ve inputted is an average of these individual scores, good luck: Motivation: 9 Clarity: 5 Novelty: 8 Memorability: 5
Really loved the art style a lot ! I think it was a great way to introduce Quadratics , Calculus and a touch of geometry !
Applying geometry to visualise the way the effects stack was so useful - would have loved to see the scope of this expanded to other areas of the game!
There is way too much Balatro terminology which is not relevant to the math (+Mult, Joker names). While some of it can be introduced, talking about “moving the blueprint to the left” while exploring the examples is confusing to people who are not familiar with the game mechanics. And maybe a bit too much backstory.
Going with the 3rd dimension would have been great to explain the trade-off between hand size and jokers (such as demonstrating why the first ectoplasm is good but the second one is very bad)
Any continuous function that has one maximum will have a slope of zero at that maximum.
That is not necessarily true, f(x)=-|x| has a maximum but no slope = 0
The last paragraph is missing the conclusion with which you started: that when t is equal to the side of the square, t=s. I.e. that it is better to balance the effects.
And it is not always possible to make a square, which happens with an uneven retriggers+scoring. This should have at least been mentioned. It is easy to see due to the simmetry that either 4x3 or 3x4 are both optimal, but the article feels incomplete.