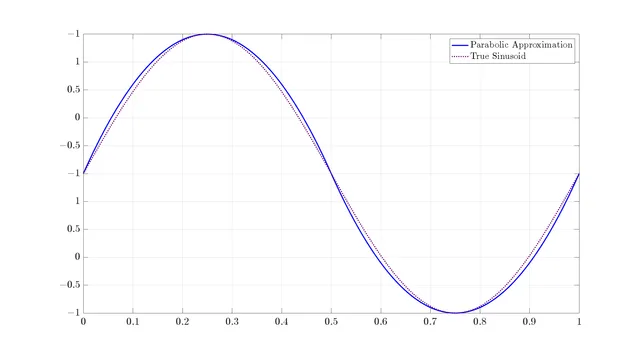
Parabolic Approximation of a Sinusoid
Audience: undergraduate
Tags: electrical-engineeringsignals-and-systemsfourier-series
A sinusoid looks quite similar to a series of truncated parabolas of alternating vertical orientation. In this blog post, I show how we can quantify how similar they really are, and then I demonstrate the implications of the differences.
Analytics
Comments
nice!
I thought this was quite clever! I’m not a mathematician, though I’m quite familiar with the Fourier series and Fourier’s trick. I didn’t follow some of the notation, but I definitely got the gist of it.
The motivation was well laid out and the plot at the very beginning was a great visualization of what we were going to discuss. I really liked the idea of comparing the fundamental to the first and second harmonics.
But the chef’s kiss was the audio clips. That was awesome and drove home that even though those two curves are very similar, they’re not quite the same and yeah, I guess our ears are very sensitive!
Kudos!
Bringing up the FT in that much detail definitely ousts any readers who aren’t already familiar with Fourier analysis, but anyone who’s familiar with it might be dissapointed to see you to omit all the important work and jump straight to the conclusion. I’d prefer that you either fully presented your work or simplified the “Fourier Series Coefficients” section to appeal to a wider audience.
Great hook at the start
Very clean layout. I felt the section on power could be motivated a bit more.
Deduct 0.1 for using j as the imaginary unit.
I’ve also wondered about this before, but didn’t look into it. Using SNR to determine the similarity is smart! The maths took some time to follow (I personally wanted to go through it step-by-step), and then hearing the difference at the end was cool!