Summer of Math Exposition
SoME4, summer 2025
The Summer of Math Exposition (SoME) is an annual competition fostering the creation of excellent math content online. You can participate as either a creator or judge. Learn more
Timeline
The competition unfolds in three phases:
- Phase 1: Join and create From to
Sign up as a participant or a judge. Creators begin working on their projects and can share progress, find collaborators, or ask for help in the Discord server.
- Phase 2: Peer Review and Voting From to
This is the heart of the event. You’ll be shown a series of entries to review, vote on, and give constructive feedback. It’s a chance to reflect, learn, and help others improve.
- Phase 3: Results and Feedback current From
The top entries and full rankings are revealed. Winners will be announced later...
Top Entries from This Year's Peer Review
A Sphere is a Loop of Loops (Visualizing Homotopy Groups)
An animated explainer on homotopy groups. It presents some geometric intuition for π₁/π₂/π₃ using loopspaces of metric spaces, in way that I don't see talked about enough. This includes an original, nonstandard visualization of the Hopf fibration.
One of the Most Powerful Math Techniques No One Knows Who Invented It
As someone who teaches mathematics to college students (or sometimes high school students I know), I've always been wishing to share something students cannot easily find in the textbook so that they can use it for problem-solving and learn mathematics in more interesting way. I believe this is one of such things that (I am pretty sure) many high school students, college students, high school math teachers, or even college math professors will find interesting to learn. I haven't seen many people who know about this property - I exchanged an email with Grant, and hopefully he remembers this very interesting ratio property of a cubic function I shared with him via email. The goal for this video is to share a ratio property of a cubic function that is very easy to remember and use for a lot of math problems involving a cubic function but still not many people know of. I wish many people get to know this ratio property of a cubic function. According to my experience, it helped me a lot when solving a polynomial equation. So, why don't you check this out? This is a very cool technique I am pretty sure a lot of people would love to learn. Thanks a lot!
The Science of Complexity
This article takes the reader on a journey into the science of emergence: the study of how simple parts can come together to create complex patterns. It begins with familiar scenes: fireflies synchronizing their flashes, schools of fish flowing as if they were liquid, and magnets uniting countless invisible atoms into a single force. Everyday wonders like these rises a profound question: how does order arise from apparent chaos? Yet the story goes beyond the phenomena themselves. In exploring the science of synchronization, the article also opens a window onto the making of theory. Science is not just a collection of ready-made answers: it is a process of building models, testing them, watching them fail, and refining them again. Here, the reader is invited to follow that process step by step. By the end, the article not only explains why such natural patterns emerge, but also offers insight into how scientists think, imagine, and persist when faced with complexity. It is at once a guide to the hidden order of the natural world and a glimpse into the patient, creative craft of theoretical science.
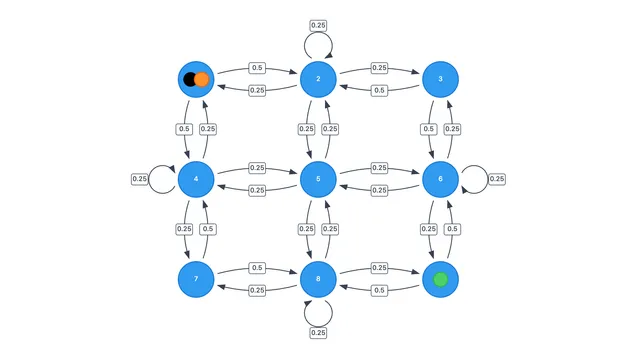
When do Markov chains converge?
The goal of this post is to present some standard Markov chain concepts (specifically, the Fundamental Theorem of Markov Chains) but make them genuinely intuitive through interactive visualizations that let you explore the ideas hands-on. This post is written for undergraduates who have some probability background. You'll get the most out of this if you're familiar with basic Markov chain concepts (states, transition matrices, etc), but even if you're not, the interactive elements should help fill in gaps, and a quick Google search or ChatGPT query can clarify anything unfamiliar.
Computer Science's Biggest Mystery
The P vs NP problem is widely agreed upon as the biggest unsolved question in computer science, asking whether discovery is harder than recognition -- if the solution to a problem is easily verifiable (like in sudoku, for example), does it also mean there’s an efficient way to find solutions in the first place? Our intuition says this should not be the case -- that solving a sudoku puzzle should be a lot harder than checking the solution once everything’s filled in. In 1956, despite the fact that computer science was a new discipline and hadn’t developed the theory and terminology we’d use today, Kurt Gödel was already pondering what the ultimate limits of computation might be, and he essentially foretold the P vs NP question 15 years before Stephen Cook would formalize it in 1971. In this video, we explore the P vs NP problem through that historical lens, thinking about the problem originally as Gödel did, in terms of a computer program trying to automatically find mathematical proofs, and eventually building up to the actual definitions of P and NP through a series of examples such as graph coloring.