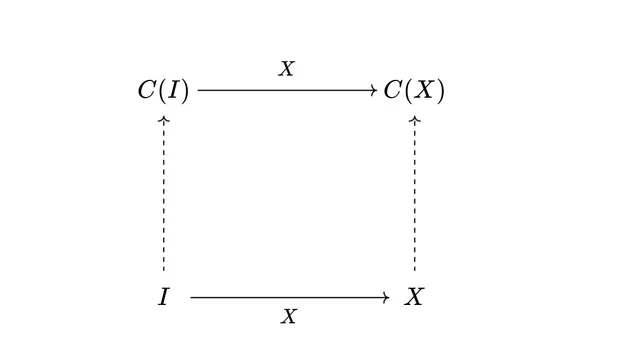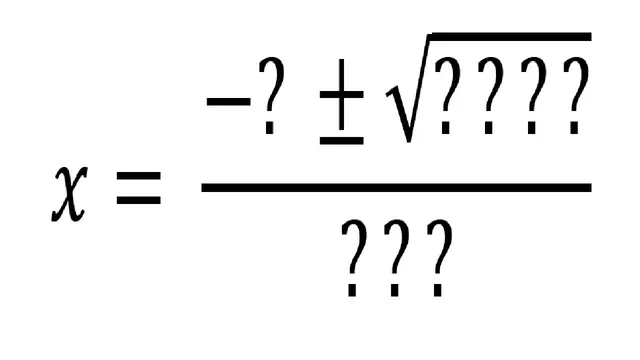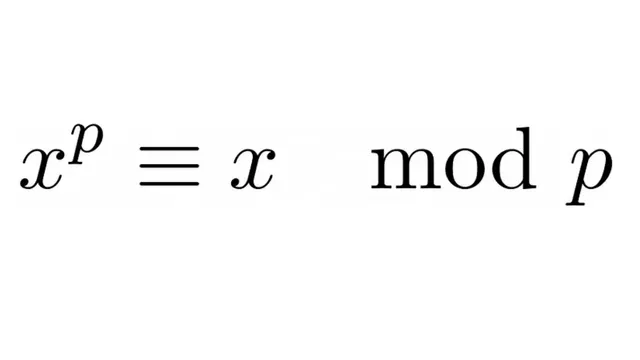Summer of Math Exposition
Archive
MaVS
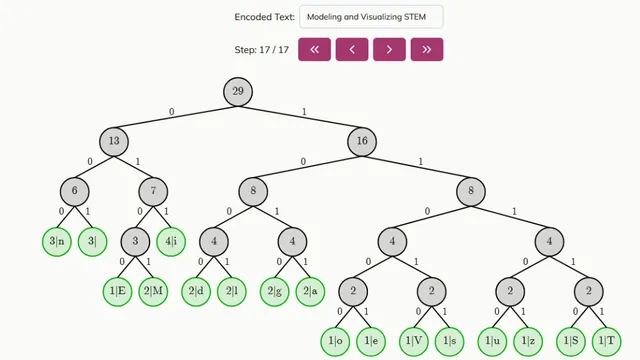
With the MaVS (Modeling and Visualizing STEM) project that our team of 3 worked on this summer, we wanted to build a website with interactive visualizations of undergraduate-level math and computer science topics. We aimed our work this summer at a few simpler topics in these fields, namely sorting algorithms, simple encoding/compression methods, and number theory (particularly modular arithmetic). We would like for the website as a whole to be evaluated as our entry, but if a single "lesson" is required as the entry, I am specifically submitting the lesson on Huffman coding.
Exploring the wave equation
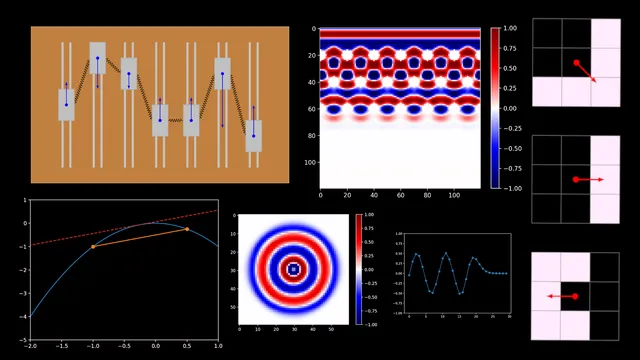
In this article, we derive and examine the wave equation in both its pure and discretized form. Finally, we build a functioning wave simulation, which allows more complex behaviour such as interaction with objects.
Math and Living Things
An interactive overview of mathematical biology written for those who are generally "mathematics-averse."
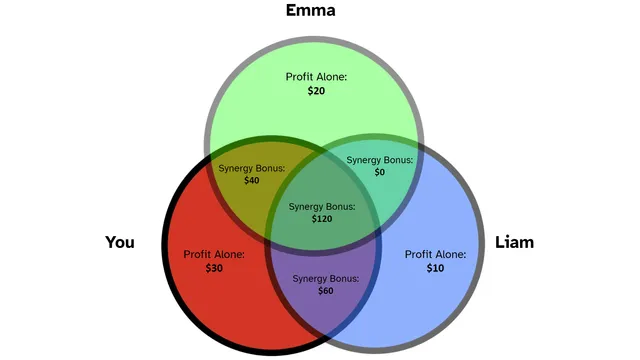
Shapley Values: Unlocking Intuition with Venn Diagrams
I stumbled upon Shapley values through my interest in explainable AI. For reference, check out the Python package 'SHAP': https://shap.readthedocs.io/en/latest/ The package analyzes the importance of each feature in a model's decision. It works for black-box models (e.g. deep neural networks), which has made SHAP extremely popular. Interestingly, very few explainers on Shapley values discuss the concept of 'synergy,' and NO explainers use Venn diagrams. I was surprised, because the visual intuition for Shapley values is simple and powerful. The value of my article lies in the gap it fills. If you're willing, I encourage you to explore the existing explainers on Shapley values and see how mine compares. Above all, this piece is a work in progress—it is my first ever online explainer, and any feedback is invaluable! Thanks so much for reading, and I hope you enjoy.
The Algebra of Socks
Delightfully, there is a way to define an algebra on the different ways you can wear your socks. In this interactive Scratch game, you solve math puzzles using a humble pair of socks and learning a little bit of group theory on the way.
Exploring Truchet Tiles and Beyond
The article explores the fascinating world of Truchet tiling and its variations. New methods are introduced to enrich Truchet tiling and to create visually interesting results. Finally, an open source Python implementation of the proposed methods is given.
Variable Rate Function Traversal (Or: How to Make Cartoons Go Faster)
A method for changing the rate at which a function is traversed over time and how it's useful for 3D animation.
Making Category Theory Relatable
Any row operation on a matrix can be implemented via left-multiplication by a fixed matrix. The way you obtain this is by applying the row operation to the identity matrix. This simple fact turns out to be an application of the Yoneda Lemma, one of the most important theorems in Category Theory. While the full statement is famously abstract, it's possible to go through the proof in this specific instance with minimal jargon. My article attempts to introduce the reader to the ideas and techniques of category theory, on the way to proving this result.
Always Check the Units Before Submitting Your Final Answer
A short story illustrating how dimensional analysis provides insight into the quadratic formula.
Transformational Music Theory: A Mathematical Approach To Analyzing Music
A primer on transformational music theory, which combines math, specifically group theory, with music theory. This post uses basic group theory and set theory, so familiarizing yourself with those fields is encouraged before reading this piece. Prior music theory knowledge is also recommended, but not required.
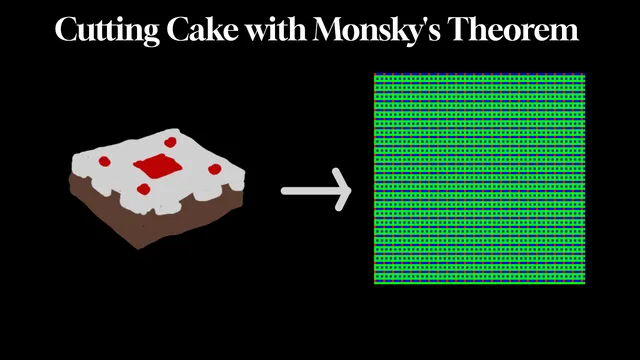
An Intuitive Explanation of Monsky's Theorem
Monsky's Theorem states that you cannot cut a square into an odd number of triangles with equal area. Despite being a seemingly simple problem about geometry, the solution draws from completely unrelated fields of mathematics, whether that be algebraic number theory or graph theory. In this blog post, I attempt to explain these connections in an intuitive manner. No higher-math prerequisites are required, although prior experience with proofs would be somewhat helpful.
Revisiting Number Theory and the Impossible Puzzle
A mathematical journey inspired by a classic sum and product puzzle. I look at solutions to the problem, and how they relate to large factors of even larger integers. Much is said about Fermat and Mersenne numbers. I look at patterns that break down, and shed new light on a topic that I previously explained in #some2. For fans of ominous horizontal scrollbars.
Fermat’s Little Theorem
An article explaining an uncommon proof of FLT that uses The Freshman's Dream. (x+y)^2 = x^2 + y^2
Interpolation in any dimension with barycentric coordinates
Interpolation is a method used to create a new point in a data set without doing new measurements, using the existing points. It can be used to create a continuous function from a set of points, and can have applications in various domains: it can be used to scale up the frame rate of a video, to predict phenomenons with less measurement, etc. In this article, we will try to find an efficient method that can handle a lot of parameters.
On the life and afterlife of proofs
An attempt at elucidating the significance of proofs in mathematics, not as a means of verification, but as a means of discovery and advance. After quickly going through different types of proof we delve into that of the Euler's conjecture. The theme of the website is "trails through the world of mathematics"
Deviation Seeker
This work present 3 algorithms on a simple problem: given a stream of data (as a string of text), determine if a single letter dominates the entire dataset.
Generalisation of Geometric Series
An article about a path of generalisation of the familiar geometric series, and its connection to combinatorics and probability, as well as analytic number theory.
How to Cheat with Math | The Russian Cards Problem
Our entry showcases the russian cards problem. This is a question about how to transfer information unencrypted whilst maintaining security. It show cases interesting ideas about the logic of knowledge. We made our entry as simple as possible.
Introduction to Group Theory 1
I am doing some research over the summer, and I wanted to explain what I am doing in a meaningful manner to my family and friends. I decided the best way to do this is to start from the ground up with Group theory, and work my way towards the specific corner of Representation Theory that my research is in. This article represents the first step in that journey. My goal is for everything to be accessible to a motivated high school (age 14-18) kid, as well as adults who haven't touched algebra in a few decades.
GoldiLooks and the Three Bearers of Optics
Introduction to Optics by GoldiLooks and the Three Bearers, providing enjoyment +/- education to a mathematically curious reader with a sense of fun. One-drive link = https://1drv.ms/b/s!AqUHOZl0LXnHjP8JZ8qyo9DUp5kaPQ
A proof of the Cauchy-Goursat theorem
This expository article presents a proof of the Cauchy-Goursat theorem along with the motivations for it. I would have liked to have some handout like this when I was taking a complex analysis course, so that is what I have attempted to make with this article. The article was written with a goal to help the reader prove the result on their own. It is aimed at an undergraduate student and assumes familiarity with some basic concepts in complex analysis.
A story about Averages
If you measure the average distance between center of a unit square and its boundary, you get exactly equal to P/4. What's P? It's the universal parabolic constant. It's like PI. but for Parabolas. But why is this problem of averages and squares... linked to parabolas? Huddle. I have a story to tell you. :) It shouldn't take long.. about 5 minutes.
Pellagons
Exploring the integer pattern that emerges from a set of simple construction rules on a hex grid.
Polynomial Regression as a Tool in Education
In this article, we look at a novel usecase of polynomial regression models.
The Snake Eyes Paradox
Blog post on a paradox in probability theory revolving around the "Snake Eyes Game": a game played by a potentially infinite pool of participants, with the actual number of participants doubling each round. Discusses multiple versions of the paradox and how they can be mathematically solved, as well as some philosophical issues relating to probability distributions over infinitely many outcomes.
Some Dusty Decades-Old OEIS Sequences
They're dusty and they're decades old. And I felt quite proud of myself for rediscovering them independently. They're part of a mathematical puzzle which is nearly a century old and has half a dozen different names. So I channelled my inner Matt Parker and Had A Go at the associated problem, and in attacking it I found I was treading paths that others followed 20 years ago and longer. Have I had any success? Probably not, but maybe. And it has been genuinely interesting to try. This entry is largely free of mathematical jargon because I'm just a hobbyist, not a trained mathematician. It should be fully accessible to any layman, and anyone who likes Numberphile videos is squarely in the target audience. I'll count it as a success if just one person grabs a sheet of scrap paper, scribbles down the same few numbers I did, and tries it for themselves. To me, that's what recreational maths is all about. And if someone makes a serious attempt at a proof by induction or a proof by contradiction at the points I've noted, I'd be delighted. [Administrivia: Because of time constraints the 'tree diagrams' in the article are not particularly clear. I will continue to try to improve them, and will insert links to improved versions when or if I manage to make them. I'm really not an artist, sadly, and it shows. I won't alter any of the text, except for typos or broken links, but I don't want to delay entering any longer.]
The Cornu Spiral
An exploration of a fascinating curve called the Cornu spiral, and a new approximation for the coordinates of the curve.
Broken Objects
Have you ever faced a challenging problem? Few things are more satisfying than discovering a simple solution to such complexities.
Adjusting for competitive advantage - a sensitivity analysis of Tenzi
This is an analysis of how competitive the dice-rolling game of Tenzi would be between kids of different ages, and to what extent adjustments to game parameters could level the playing field. Inline visualizations were generated with Python.
Accuracy of an Epicycle Model for Predicting Eclipses
This is a blog post where I try to determine how accurate a simple epicycle model can be for predicting lunar and solar eclipses. Using code, I show how to determine the parameters with Hipparchus' method, and show how these parameters compare to modern values based on an elliptical orbit. The resulting parameters for the sun and moon are then used to predict the eclipses and compare them to modern predictions. One potential advantage of an epicycle model is the easier to calculate by hand, especially in the days where astronomers used tables to determine the positions of the sun and moon.
Ramblings on Malliavin Calculus
This entire web book was created so I can explain the topics of Malliavin Calculus and the Clark-Ocone formula to myself. After many months of frustration, I figured the main obstacle with learning the topic is the emphasis on mathematical rigor over pedagogical clarity, so I hope to bridge that gap. I’m assuming just basic knowledge of algebra, analysis and probability. I start with developing what Malliavin calculus was meant to address. I approach it in an indirect, meandering way. After documenting situations were a problem exists, the need for a solution will generate a “vacuum” of sorts. Following that, again indirectly, I lay the foundation step by step. Finally, the vacuum is filled. As mentioned, pedagogical clarity is the guiding factor. I’ll disregard proofs if I don’t see them important. Shortcuts will be taken liberally. Some pieces will lead nowhere or be there just to round up a concept. I may even admit when I’m ignorant about something and leave it like that. Truth is, I’m not a mathematician, a statistician or an economist. I’m just trying to understand an obscure topic.
Solving Lights-Out
In this presentation, I cover: - The mechanics of the Lights Out game - A playable demo - Solving the game (RREF over Z_2) - Solvability of a game - (crux.) Size and Shape doesn't matter - Create your own lights out grid, and have the program solve it! - Proof that the all lights-on configuration is always winnable The content in this presentation is heavily inspired from this snippet (https://njohnston.ca/lights_out.pdf) from the book "Introduction to Linear and Matrix Algebra" authored by Nathaniel Johnston This is an interactive presentation built using Python, Jupyter and RISE. It requires the viewer to execute every code-cell (Using ctrl+enter). The slides are browsed using the Pg-Up and Pd-Dn buttons respectively. On some monitor resolutions the content may overflow; please use ctrl + - to adjust accordingly. The level creator for the lights out game used at the end currently supports only mouse events and not touch. Find the repository for the presentation here: https://github.com/iamviveksrk/LightsOut The submitted link is a mybinder link to the project, which will automatically open it in presentation mode. It may take about a minute to load the containers and begin.
A Sketch of a Nonexistent Pyramid
In this exposition, we present a theorem and a sketch of its proof. This theorem extends the renowned Gelfand-Mazur Lemma from the theory of normed algebras. Familiarity with the context—the theory of unitary Banach C-algebras—is assumed. The original lemma states: "If $A$ is a unitary Banach C-algebra, for any element $a \in A$, there exists a complex number $\lambda$ such that $a - \lambda$ is non-invertible in $A$." The generalization is as follows: "If $A$ is an R-algebra and $E$ is an R-vector subspace of $A$ where all elements commute, and any nonzero element of $E$ is invertible in the completion $\hat{A}$ of $A$, then $E$ has at most two independent vectors." Here, $R$ denotes the real number field.
Hertzsprung Series
Just a little recap and research on the hertzsprung series on the OEIS. If you choose to go the itch.io page; the paper is new, the game is old, I hope that doesn't disqualify me.
Graph Colouring with Group Theory
I tried to constrain myself to one page. This document shows a connection between graph theory and group theory, allowing one to transfer computability results from k-colouring to a certain class of problems in group theory. Unfortunately, due to the one page constraint, I did not make certain notions precise, but I hope the reader can still make out the main ideas.
A Delicious Theorem in Analysis
Some applications of the intermediate value theorem that can be done in a kitchen.
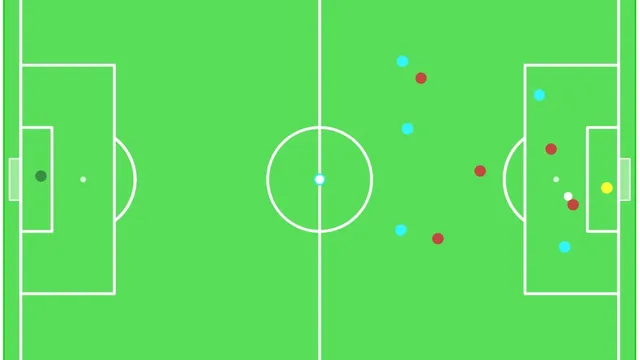
World in Motion: How to animate the beautiful game
In a Summer full of wonderful sporting moments, we wanted to recreate our favourite: the goal that won the FA Cup! Feeling a little nostalgic, we thought it would be fun if our virtual Soccer highlights took on the appearance of a retro video game. To our surprise, a simple application of High School mathematics provided a short-cut. Here, we outline an approach that can easily be adapted to animating highlights from the NFL, NHL, MLB, NBA, and many other sports besides. And if you're not a big Sports fan, we hope you'll enjoy dreaming up new ways to apply a powerful animation technique!
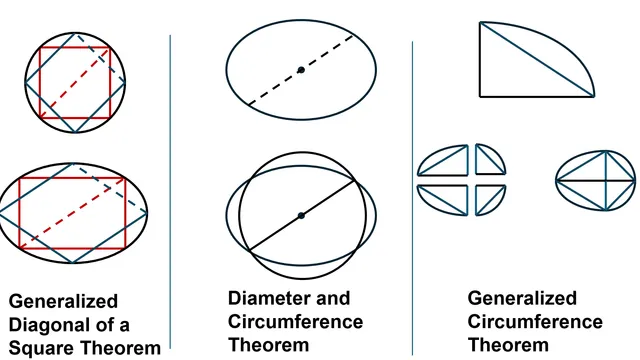
Ellipse Theorems – Defining Perimeters and Reshaping Geometry
This Paper defines three new ellipse theorems. The three theorems are as follows: • The Generalized Diagonal of a Square Theorem • The Diameter and Circumference Theorem • The Generalized Circumference (round shapes) Theorem The implications of these theorems are as follows: • An exact ellipse circumference equation (closed form) • A unification of the ellipse and circle equations for circumference and area • A new group of rounds shapes with defined circumference and area equations This is a link to the accompanying Desmos Graph - https://www.desmos.com/calculator/bkr35tpff9 Everything explained in the paper is interactively demonstrated in the graph.
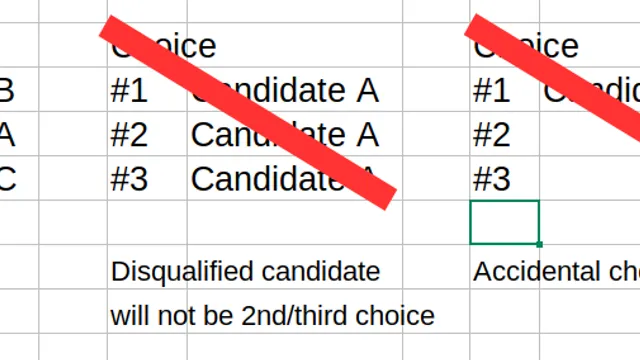
Ranked-choice (Instant-runoff) Voting, Interactive Demo
In the US, many people want ranked-choice voting as an alternative to the current system where a candidate may win even with less than half of the total votes. View this interactive demo to see how Rank-choice voting can allow third party candidates a better mathematical possibility of winning.
A Beginner's Guide to Graph Theory
A basic illustrated guide to the principles of graph theory which has many applications in computer science and the natural sciences.
How to crochet a Rolling Torus
Yes! You can actually crochet a torus that can roll around its circular axis! Once you get the hang of it, you can now create your own smoothly rolling toruses in all shapes and sizes and explore firsthand how a tiny change in pattern may result in a very different outcome. This new technique is a must for crochet artists and mathematicians alike - you can now explore torus knots and links by pure craftsmanship.
Can We Calculate the Day That We WILL Die?
Quantifying death as a side quest
Permutation Tables, Permutation Cycles and Transpositions
This article (and associated articles) explains you how Linear Permutation Without Repetition of N Distinct Items can be mathematically represented
The Mysterious Primal Music of Like Powers Summed
Together we are uncovering the hidden math gems within the counter-examples to the Euler sum of like powers conjecture. Check out one of the math diary entries. Let the treasure hunt continue!
Green’s Theorem Application – Volume : Prism + Cutting Plane
Finding volume of a prism cut by a plane using Green's Theorem.
Riemann-Liouville Integral and Mellin Transform
In this paper I would like to introduce the generalized multiple integral,Riemann-Liouville integral, and see its application on special functions, such as Gamma function and Zeta function, by using Mellin Transform.
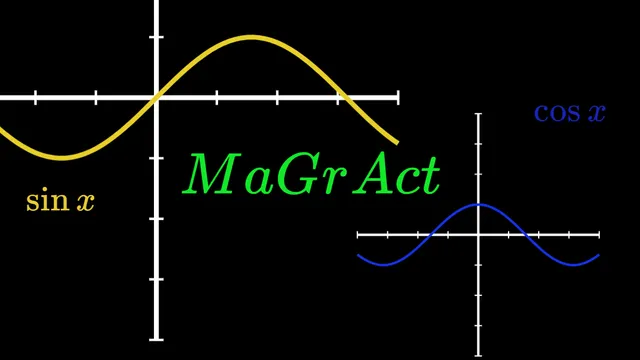
MaGrAct - Mathematical Graphic Action
MaGrAct wants to be a tool to create beautiful maths related animations. The goals for this tool are: - to be simple: a user should be able to pick up 70% of how the tool works from the get-go - to be powerful: lot of features and things to draw - to have a clear and nice UI This was built keeping in mind Manim. Of course, it's not as powerful and still in early stages, but I think it might have potential. :) Here is the link of the repo (in the link section I have set the link to go directly to the web app) https://github.com/lolloz98/MaGrAct
Leveraging Floating Point Representation to Efficiently Calculate x^(1/m) without Special Operations
In 1999, an unintuitive method was employed in the Quake III Arena graphics library to quickly calculate surface normals for lighting and shading. I will expand this method to calculate x^(1/m), where m is a non-zero integer, as well as for other approximate exponential calculations. For example, if m=−1, the calculation becomes a division. The method uses floating point representation to find an initial guess, followed by one or two steps of the Newton-Raphson method.
Analytic Solutions to Myer’s Theory of Gravity
Quantum mechanical analogue to the classical theory of gravity proved
Math Resource Center
The Math Resource Center is a website that contains links to the best math educational resources on the internet.